ABC172の参戦記。
今回もAB2完でした。C問題が今回も解けなかった。
C問題のコンテスト中に提出したアルゴリズムは間違ってるし、書いたコード自体も間違ってて、ダメダメでしたが、解説を見て、自分でコードを書いてみていろいろと学ぶことがありました。
今回もABC172のA-CのPython3でのコードと、pythonの標準ライブラリである、bisectとリストを操作した場合の実行時間の比較するコードが最後にあります。
A – Calc
入力を受け取って、計算したものを出力する問題。
Python3では、累乗計算を以下の方法で書けますね。
Python3はpowで計算した数字も整数で返せるならint型で返ってきますね。(この記事書いてる中で知りました。)
a*a
a**2
pow(a,2)3乗の計算は同様に、以下のいずれかで可能です。
a*a*a
a**3
pow(a,3)これらを計算して標準出力すればOKです。
私は、a**2 a**3 で書いて提出しました。
a=int(input())
print(a+(a**2)+(a**3))B – Minor Change
文字列の長さが一緒なことが保証されているので、入力された文字のi番目が一緒かどうかを順番に調べていって、もしも違ったら、書き換える文字数が1つ増えたことにして、最後まで調べた結果を出力すればOK。
S=input()
T=input()
N=len(S)
ans=0
for i in range(N):
if S[i]==T[i]:
pass
else:
ans+=1
print(ans)C – Tsundoku
今回も解けなかったC問題。
理解するまでを時系列で書きます。
コンテスト中の思考回路
- AとBの積読の山の一番上から順番に読む。
- 読むのに必要な時間が短いものをたくさん読む。
この2点から、常に読む時間が短い(もしも一緒の場合は、短い時間の本がある)ほうを選択し続ければよい。と思い、貪欲法で解こうとしました。
蟻本で貪欲法は設計に気を付ければ、効果的なアルゴリズムですというような感じで書かれていたので、これはちょうど貪欲法で解ける問題だー!と思いこんでしまいました。
ちなみに、貪欲法でダメなことが分かったのはコンテスト後、暫く経ってからです・・・
貪欲法でダメな例は、例えば次のような場合です。
N,M,K=5,5,10
list_a=[5,5,5,5,5]
list_b=[6,1,1,1,1]このような場合は、明らかにlist_bから5冊読むのが良いのですが、上で書いたような貪欲法だとlist_aから2冊読んで終わってしまいます。
こんな単純なNG例にもコンテスト中には気づかずにいるので、ダメダメですね・・・
解説を確認したのちに試したこと(累積和と配列操作(append,sort,index,count))
解説をざっと見て、解法の方向性を確認しました。
なるほど、Aの山から〇〇冊読んだ場合の、Bの山から読める最大の冊数を数えて、両方の机から読んだ冊数の最大値を答えとすればよいのか。
キーワードは、「累積和」、「二分探索」の模様。(「尺取り法」は制御が難しそうなので今回は見送ります。)
累積和は、0だけが入った新しいリストを用意して、元のリストの足したい要素と、新しいリストの一番後ろの値を足して作れることが分かったのでこれを作ります。
list_a=[1,2,3,4,5]
Accumulative_sum_array=[0]
for a in list_a:
temp_a=Accumulative_sum_array[-1]+a
Accumulative_sum_array.append(temp_a)
print(Accumulative_sum_array)
# >> [0, 1, 3, 6, 10, 15]Aの山だけで累計がKを越えるものはどうやっても読めない部分だから、最新の値がKを越してたら処理を抜ける。そして、この累積和の要素数が探索する件数になります。
このAの累積和の各値をKから引いた値がBの山に使える時間です。
Bの累積和の配列に、上で求めたBの山で利用できる時間を追加(append)して、ソート(sort)後に、Bで使用できる時間の要素番号を見つけたら(index)、その一個前がBの山で読める冊数です。
もしかすると、Bの山に使える時間ちょうどに読み終わる場合があるかもしれません。
その時は読める冊数を+1すればOKです。
これで、Aの山から読んだ冊数を1つ増やしてBの山で読める本の数を調べていって、最大値を求めていければOKと考えました。
この手順をコードにして提出したら、大量のTLE。。。
配列の操作を多くするとPythonは遅くなるんですよね。
はい。知ってます。
Bの山の探索に二分探索(bisect)を利用
for文の中で、配列の操作を多用するのは処理時間が長くなるので、上でもあげた二分探索を利用することにします。
二分探索は、単調増加の配列に、特定の数字がどこに位置するかを調べるのに有効な手段です。
私は、少し前の精進で、ABC146-C(C – Buy an Integer)で実装したのですが、私にとっては結構重たいコードだったので、気が進まなかったのですが、アルゴリズムとしての力は実感もしていました。
たしかPythonに二分探索のライブラリがあったような気もするので、調べてみたらやはりありました。
bisect
なんかビスケットみたいで美味しそうな名前のライブラリだなー。って思っていたやつです。
二分探索は英語でbinary searchなので、略すとしたらbisechでしょうに、なんでhじゃなくてtなん?って思っていたら、
bisectで「二分する」っていう動詞でした。貧弱な英語力。。。
さて、気を取り直してbisectのドキュメントを読んでみると、同じ値がある場合には左側に入れるのか、右側に入れるのかを選択できるらしい。まさに上でも書いた通り、Bの山に使える時間ちょうどに読み終わる場合が、一発でわかるってことですね。
import bisect
list=[10,20,30,40,50]
a=bisect.bisect_right(list,50)
print(a)
# >> 5.bisectのみでも.bisect_raightと同じ動きをするようですが、私は明示的にわかりやすい.bisect_raightを使用しようと思います。
ちなみに左に入る場所が知りたい場合は.bisect_raightの部分を.bisect_leftにすればOKです。
import bisect
list=[10,20,30,40,50]
a=bisect.bisect_left(list,50)
print(a)
# >> 4配列操作するコードのfor文の中をこのbisectを利用したものに置き換えて提出すると、ACになりました。
今回のACしたコードはこれです。
import bisect
N,M,K=map(int,input().split())
list_a=list(map(int,input().split()))
list_b=list(map(int,input().split()))
#Aの山の累積和を作成(Kを超えたらSTOP)
totaltime_a=[0]
for a in list_a:
temp_a=totaltime_a[-1]+a
if temp_a>K:
break
else:
totaltime_a.append(temp_a)
totaltime_b=[0]
for b in list_b:
totaltime_b.append(totaltime_b[-1]+b)
ans=0
for i in range (len(totaltime_a)):
Kb=K-totaltime_a[i]
j=bisect.bisect_right(totaltime_b,Kb)-1
if i+j>ans:
ans=i+j
else:
pass
print(ans)Appendix ~おまけ~
今回、for文の中で配列操作したコードと、二分探索を利用したコードで、どれだけ違いがあるのかが気になって調べてみました。
実行環境は、Googlecolaboratryです。
問題文中の制約の中でランダムで値をとってきています。AとBの累積和で、Kを越す値になるのをコントロールするために、それぞれの値が取りえる範囲をどんどん狭めています。
下の図の、棒グラフの上段が二分探索でかかる時間。下段が配列操作でかかる時間です。
それぞれ1000回実行した結果の平均時間をとっています。
標準偏差や95%信頼区間も表現したかったけれどもうまく表現できませんでした。
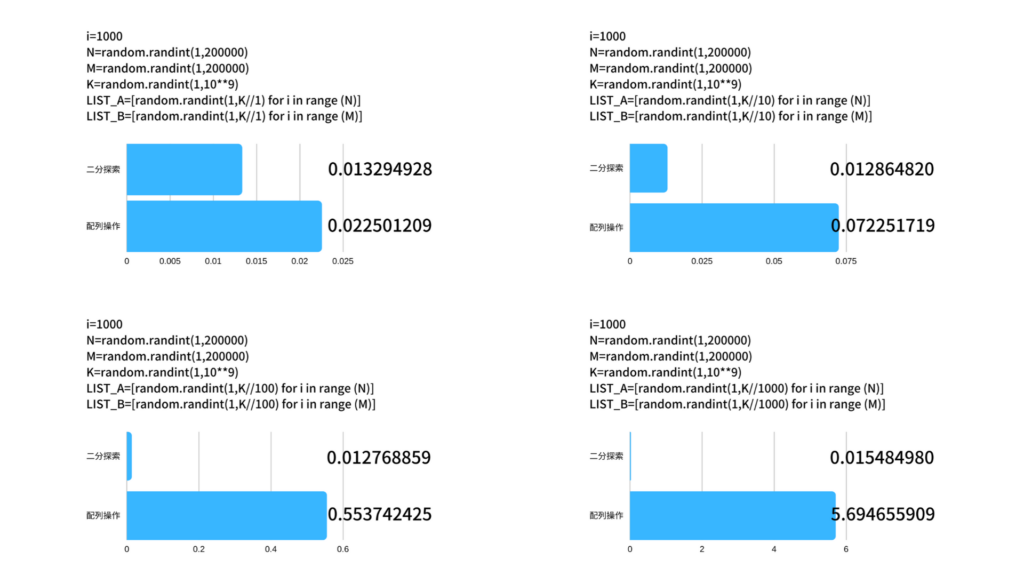
問題文中の、Aの配列、Bの配列の各要素の数字が小さい(つまり、AのKまでの累積和の配列の要素が多い)場合、明らかに配列操作の方が時間がかかっていることが分かりますね。
一方、二分探索はAやBの配列、累積和の要素数が多くなっても、処理する時間の桁が1つ増えるということもありません。
bisectすごい!!!
ビスケットみたいな名前なのに。。。w
以下に私が確認ように使用したコードを貼っておきます。
def ABC172_C():
import time
import random
O_N=random.randint(1,200000)
O_M=random.randint(1,200000)
O_K=random.randint(1,10**9)
LIST_A=[random.randint(1,O_K//100) for i in range (O_N)]
LIST_B=[random.randint(1,O_K//100) for i in range (O_M)]
'''
↑↑問題設定↑↑
----------------------------
↓↓二分探索↓↓
'''
N=O_N
M=O_M
K=O_K
list_a=LIST_A
list_b=LIST_B
start1=time.time()
import bisect
totaltime_a=[0]
for a in list_a:
temp_a=totaltime_a[-1]+a
if temp_a>K:
break
else:
totaltime_a.append(temp_a)
totaltime_b=[0]
for b in list_b:
totaltime_b.append(totaltime_b[-1]+b)
ans1=0
# laptimelist1=[]
for i in range (len(totaltime_a)):
# laptime_start=time.time() #for文タイム計測
Kb=K-totaltime_a[i]
j=bisect.bisect_right(totaltime_b,Kb)-1
if i+j>ans1:
ans1=i+j
BOOK_A=i
BOOK_B=j
else:
pass
# laptime_finish=time.time() #for文タイム計測
# laptimelist1.append(laptime_finish-laptime_start)
# print(ans1)
process_time1 = time.time() - start1
# print(laptimelist1)
# print(process_time1)
'''
↑↑二分探索↑↑
----------------------------
↓↓配列操作↓↓
'''
N=O_N
M=O_M
K=O_K
alist=LIST_A
blist=LIST_B
start2=time.time()
A_total=[0]
for a in alist:
_a=A_total[-1]+a
if _a>K:
break
else:
A_total.append(_a)
B_total=[0]
for b in blist:
B_total.append(B_total[-1]+b)
ans2=0
# laptimelist2=[]
for i in range (len(A_total)):
# laptime_start=time.time() #for文タイム計測
Kb=K-A_total[i]
temp_Btotal=B_total
temp_Btotal.append(Kb)
temp_Btotal.sort()
j=temp_Btotal.index(Kb)-1
if temp_Btotal.count(Kb)==2:
j+=1
if i+j>ans2:
ans2=i+j
# laptime_finish=time.time() #for文タイム計測
# laptimelist2.append(laptime_finish-laptime_start)
# print(ans2)
process_time2 = time.time() - start2
# print(laptimelist2)
# print(process_time2)
return '0',O_N,O_M,O_K,ans1,process_time1,ans2,process_time2,'0'
print('_,{0},{1},{2},{3},{4},{5},{6},_'.format('N','M','K','ans1','time1','ans2','time2'))
for i in range(1000):
a=ABC172_C()
print(a)



コメント