この日は週末に久々に晴れた日で畑の雑草を処理して体力使い果たした土曜日。
昼寝して体力回復してからコンテストに臨みました。
開催前に配点を確認したらABCと同じ感じのスコア配分なことが分かったので、C問題くらいまでできると良いなと思いながら臨んだコンテストですが、今回”も”C問題が解けずに終わりました・・・。
正解一歩手前までいってたけどTLE恐怖症により3重ループのfor文を提出しなかった。しかし、実際には余裕で間に合った。という落ち。コンテスト後の解説pdfをチラ見して途中まで書いていたコードに追記して提出したら何事もなくACしました。
(2020/07/13追記:取消線)
今回の記事も、A-C問題のPython3でのACコードとおまけつき。おまけは、print出力がいかに実行処理時間がかかるか。という結構しょーもない(けど結構重要?な)話です。
おまけは、print()の処理を画面に表示するのに結構時間がかかる。という話です。
A – Number of Multiples
for文と、倍数判定の問題。
for文で判定する数字の区間をどうするかで、方針は分かれると思いますが、私は、for文の開始の数字をLとする方針としました。
ほかの方法としては、for文のスタートは0からとして、判定する数字の方で、Lを足す方針でもOKですね。
倍数判定は、dで割った時の余りが0であれば倍数として判定できます。
倍数判定はfizzbuzz問題が有名ですね。
for文の中で、倍数判定がTureの時の個数をansとして数えて、最終的なansの数を出力すればOKです。
私がコンテスト中に書いたコード
L,R,d=map(int,input().split())
ans=0
for i in range(L,R+1):
if i%d==0:
ans+=1
print(ans)for文のスタートは0からとして、判定する数字の方でLを加算する方針でのACコード
L,R,d=map(int,input().split())
ans=0
for i in range(R-L+1):
if (L+i)%d==0:
ans+=1
print(ans)B – An Odd Problem
リストの取り扱いと、for文、偶奇判定の問題。
リストに含まれている要素のうち、1個飛ばしで処理する方法については、私は3つくらい思いつきますが、一番実装で安全そうな1を選択しました。
一番Pythonicなのは2だと思います。
- 1個飛ばししたリストを新たに作成して、全部判定する。
- for文の判定する要素を1個飛ばしで判定する。
- for文で、iが奇数の場合はcontinueして、全部判定する。
偶奇判定は2で割った余りが、0は偶数、1は奇数ですね。
偶奇判定で奇数だったものの個数を数え上げていって、答えを出力したらOKです。
私がコンテスト中に書いたコード。(上記リストの1)
N=int(input())
ai=list(map(int,input().split()))
ai=ai[::2]
ans=0
for i in range(len(ai)):
if ai[i] %2==1:
ans+=1
print(ans)おそらく一番Pythonicなコード(上記リストの2)
N=int(input())
ai=list(map(int,input().split()))
ans=0
for a in ai[::2]:
if a%2==1:
ans+=1
print(ans)for文の中で判定要素を飛ばすコード(上記リストの3)
N=int(input())
ai=list(map(int,input().split()))
ans=0
for i in range(N):
if i%2==1:
continue
if ai[i] %2==1:
ans+=1
print(ans)C – XYZ Triplets
全探索した結果をリストとして保持して、リストの要素を順番に出力する問題。
n<=10**4ということ。与えられた式(x**2+y**2+z**2+xy+yz+zx)から、x,y,zが取りえる範囲はそれぞれ100未満だということが分かります。
x,y,z=100,1,1 の場合、n=10,203となり、10,000(10**4)を超えてしまうからです。
x,y,zの組み合わせの順番は関係なく、x,y,z=1,100,1でも、x,y,z=1,1,100でも同様にn=10,203となります。
x,y,zをそれぞれ1-100までの間のfor文でループして、それぞれの値から導き出されるnに組合わせパターン数を記録していって、Nまでのパターンを出力したらOK。
解説pdfをチラ見して、3重ループのfor文でOKなことを確認して、提出したらあっさり通りました。
def f(x,y,z):
n=x**2 + y**2 + z**2 + x*y + y*z + z*x
return n
N=int(input())
anslist=[0]*60100
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
n= f(x,y,z)
anslist[n-1]+=1
for i in range(N):
print(anslist[i])コンテスト中に3重ループのfor文を提出しなかったのが悔やまれます。
上記の通り、x,y,zの取りえる値は100(10**2)までということがわかっているので、3重ループしたとしても、100*100*100=1,000,000(10**6)で、十分に間に合う計算量です。
私がなぜ、TLEを恐れて3重ループの全探索をせずに、ほかの解法を探ってしまったかというと、3重ループのfor文を実際にprintしてしまったからだと思います。
なぜそんなことをしたかというと、
過去問を解いている中で、答えの分布がどうなるのかを知るためには、実際に組み合わせのパターンがどのような値になるのかをシミュレーションしてみるのが良さそうなことがわかりました。
具体的には、ABC165-D(Floor Function)です。
この問題を解くときのカギとなったのは、実際にいろいろな数字でシミュレートしてみて答えが出せたので、今回も実際にx,y,zを100までの数字でnがどうなるのかをシミュレーションしてみました。
その時の様子がこちら。(xが25になるくらいまでなので、全体の1/4程度です。)
これをみて、
「やっぱり3重ループは処理実行時間かかって、これは制限時間内に終わるのは無理だ。」
と思ってしまったのですよね。
ここから、(x+y+z)**2=x**2+y**2+z**2+2xy+2yz+2zxと今回のn=x**2+y**2+z**2+xy+yz+zxの差を考えるなど、どんどん迷走していって、結局コンテスト中に提出できませんでした。
Appendix ~おまけ~
今回、シミュレーションした結果、3重のfor文が間に合わないと感じた件、標準出力するのがどれくらい実行速度に与える影響があるのかを調べてみました。
N=10**4の最大ケースで調べています。
実行環境は、Googlecolaboratryです。
まずは、私がシミュレーションにて使用したプログラムはこれで計測。
import time
def f(x,y,z):
N=x**2 + y**2 + z**2 + x*y +y*z +z*x
return N
s=time.time()
for a in range(1,100):
for b in range(1,100):
for c in range(1,100):
if f(a,b,c)<=10**4:
print(f(a,b,c),a,b,c)
f=time.time()
print(f-s)実行結果
6 1 1 1
11 1 1 2
18 1 1 3
27 1 1 4
~~~
...略...
~~~
9915 97 4 1
9803 98 1 1
9905 98 1 2
9905 98 2 1
135.63258957862854実行結果は明らかに間に合わない・・・
次に、ACしたコードにtimeを埋め込んでみました。
def f(x,y,z):
n=x**2 + y**2 + z**2 + x*y + y*z + z*x
return n
import time
s=time.time()
N=10000
anslist=[0]*60100
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
n= f(x,y,z)
anslist[n-1]+=1
for i in range(N):
print(anslist[i])
f=time.time()
print(f-s)実行結果はこちら
0
0
0
0
0
1
0
0
0
0
3
0
0
0
0
0
3
3
~~~
...略...
~~~
15
75
48
36
18
48
24
36
36
54
15
108
0
84
18
2.6433773040771484(2020/07/13追記:取消線)あれwこれきっとテストケースのNは10**4じゃないですねw
(2020/07/13追記)
指摘していただきました。
すいません。誤情報を書いていたみたいです。
print()自体の処理にはあまり時間がかからないが、print()したものを画面に表示するのに時間がかかり、上記のような結果になっているようです。
たきお(@tachyon_kpr)さん、ありがとうございます!
全探索で、答え用のリストを作るまでの時間を計測してみましたw
def f(x,y,z):
n=x**2 + y**2 + z**2 + x*y + y*z + z*x
return n
import time
s=time.time()
N=10000
anslist=[0]*60100
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
n= f(x,y,z)
anslist[n-1]+=1
f=time.time()
a=f-s
for i in range(N):
print(anslist[i])
print(a)実行結果はこちら
~~~
...略...
~~~
54
15
108
0
84
18
1.3576478958129883実際のNはどのあたりなのかな?と探ってみた結果はこちら
def f(x,y,z):
n=x**2 + y**2 + z**2 + x*y + y*z + z*x
return n
import time
s=time.time()
N=5000
# N=4000
anslist=[0]*60100
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
n= f(x,y,z)
anslist[n-1]+=1
for i in range(N):
print(anslist[i])
f=time.time()
print(f-s)実行結果はこちら
N=5000
# >> 2.044497013092041
N=4000
# >> 1.897986888885498
(2020/07/13追記:取消線)コンテストのテストケースはN=4000とか3000くらいだったのかなー。
(2020/07/13追記)
上記の実験は、print出力で画面に表示される時間を含んでいるため、実行時間が遅くなっているように見えますが、実際にプログラム上で出力するのにはそんなに時間はかからないようです。
実際のテストケースのNの値を探ってみました。
どうやら、N>9900なことは間違いなさそうです。
今回得られた教訓は、
(2020/07/13追記:取消線)標準出力するのにも時間がかかる!
(2020/07/13追記)
標準出力自体の時間は短いが、出力を画面に表示するのには時間がかかる!
計算量の見積はちゃんと理論値で行おう!
(2020/07/13追記)
ブログに嘘書かない!
教えてもらえるってすごくありがたい!
たきおさんありがとうございます!!
(2020/07/13追記:取消線)ってことですかね!?
(2020/07/15追記)
まにゃpy(@uuyr112)さんに教えていただいたPythonのモジュールの一つ、line_profilerをインストールして実施してみました。
print()の出力を画面に表示しない方法についてはググってみて、以下のコードで実現させています。
import os
from contextlib import redirect_stdout
def main():
print(0)
if __name__=='__name__':
main()
with redirect_stdout(open(os.devnull,'w')):
main()
# >>
# 0が表示されない。line_profilerによる、各行の実行結果の判定用のコードです。
まずはprint()の出力を画面に表示させるコードをためします。
from line_profiler import LineProfiler
import os
from contextlib import redirect_stdout
def f(x,y,z):
n=x**2 + y**2 + z**2 + x*y + y*z + z*x
return n
def main():
N=10**4
anslist=[0]*60100
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
n= f(x,y,z)
anslist[n-1]+=1
for i in range(N):
print(anslist[i])
if __name__=='__name__':
main()
# print()を画面出力する。
prof = LineProfiler()
prof.add_function(main)
prof.runcall(main)
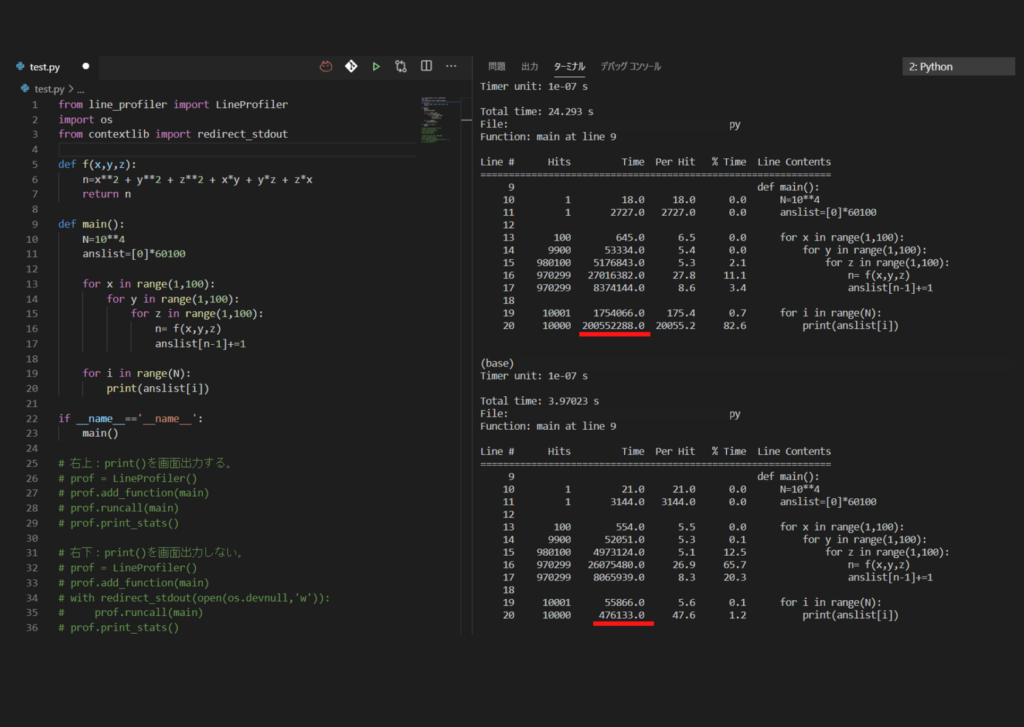
prof.print_stats()実行結果はこちら
...略...
108
0
84
18
Timer unit: 1e-07 s
Total time: 24.293 s
File: c:/Users/〇〇/test.py
Function: main at line 9
Line # Hits Time Per Hit % Time Line Contents
==============================================================
9 def main():
10 1 18.0 18.0 0.0 N=10**4
11 1 2727.0 2727.0 0.0 anslist=[0]*60100
12
13 100 645.0 6.5 0.0 for x in range(1,100):
14 9900 53334.0 5.4 0.0 for y in range(1,100):
15 980100 5176843.0 5.3 2.1 for z in range(1,100):
16 970299 27016382.0 27.8 11.1 n= f(x,y,z)
17 970299 8374144.0 8.6 3.4 anslist[n-1]+=1
18
19 10001 1754066.0 175.4 0.7 for i in range(N):
20 10000 200552288.0 20055.2 82.6 print(anslist[i])続いて、print()の出力を画面に表示しないコードはこちら。
(最後の実行部分のみ違います。)
from line_profiler import LineProfiler
import os
from contextlib import redirect_stdout
def f(x,y,z):
n=x**2 + y**2 + z**2 + x*y + y*z + z*x
return n
def main():
N=10**4
anslist=[0]*60100
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
n= f(x,y,z)
anslist[n-1]+=1
for i in range(N):
print(anslist[i])
if __name__=='__name__':
main()
# print()を画面出力しない。
prof = LineProfiler()
prof.add_function(main)
with redirect_stdout(open(os.devnull,'w')):
prof.runcall(main)
prof.print_stats()実行結果はこちら。
Timer unit: 1e-07 s
Total time: 3.97023 s
File: c:/Users/〇〇/test.py
Function: main at line 9
Line # Hits Time Per Hit % Time Line Contents
==============================================================
9 def main():
10 1 21.0 21.0 0.0 N=10**4
11 1 3144.0 3144.0 0.0 anslist=[0]*60100
12
13 100 554.0 5.5 0.0 for x in range(1,100):
14 9900 52051.0 5.3 0.1 for y in range(1,100):
15 980100 4973124.0 5.1 12.5 for z in range(1,100):
16 970299 26075480.0 26.9 65.7 n= f(x,y,z)
17 970299 8065939.0 8.3 20.3 anslist[n-1]+=1
18
19 10001 55866.0 5.6 0.1 for i in range(N):
20 10000 476133.0 47.6 1.2 print(anslist[i])print()出力を画面に表示するのがいかに時間がかかっているかがわかります。




コメント