先週はABC開催されなかったため、1週間間をあけてのコンテスト。
最近JSの学習していて、1週間ほどPythonのコードを書いてませんでした。
金曜日から競プロの練習再開したら昔解けなかった問題もすんなり解けて、「お、なんか調子良いな。」と思いあがりながら臨んだABC178でした。
前回はB問題で苦戦してC問題も解けなかった灰色コーダーが、自分の復習のためにもABCの参加記録を残しています。
使用言語はPython3で、A問題からC問題までのACコード付きです。
A – Not
標準入出力とif文の問題。
比較演算子のx==1の部分が、代入の=と混同しないようにするのが注意点でしょうか。
# AtCoder Beginner Contest 178
# A - Not
x=int(input())
if x==1:
print(0)
else:
print(1)上級者の方はbit演算のXORとかを利用したりするかと思います。
1行で通りますが、コンテスト中に私はこれを書けないです。
print(int(input())^1)B – Product Max
最大値を求める問題。
xとyが取りうる範囲がそれぞれマイナスからプラスになるために、それぞれの場合分けが必要かと考えたのですが、答えとなるのは、a*cまたはa*d、もしくは、b*cまたはb*dとなります。
これらの中から最大値を出力すればOKです。
# AtCoder Beginner Contest 178
# B - Product Max
a,b,c,d=map(int,input().split())
print(max(a*c,a*d,b*c,b*d))C – Ubiquity
包含と排除の原理(包除原理)を問われる問題。
今回もC問題をコンテスト中に解けませんでした。
コンテスト中は、0と9が存在する数字の組み合わせから重複する組み合わせを引けば行けるかと思っていたのですが、うまくいかず時間切れになりました。
全ての数字の組み合わせから、0が存在しないパターンと9が存在しないパターンの場合をひいて、引きすぎている0と9がともに存在しない場合が足せば答えになる。という問題です。
N桁の整数列は10**N通りで、0で存在しない数列は9**N通りで、同様に9が存在しない数列も9**N通りとなります。
ただ、0が存在しない数列の中には、9が含まれない数列も存在し、同様に、9が存在しない数列の中に、0が含まれない数列が存在しているので、全体からこれらを引くと、0も9も存在しない数列の8**N通りを引きすぎていることになるため、その分を加算します。
ベン図で書くとこうですね。
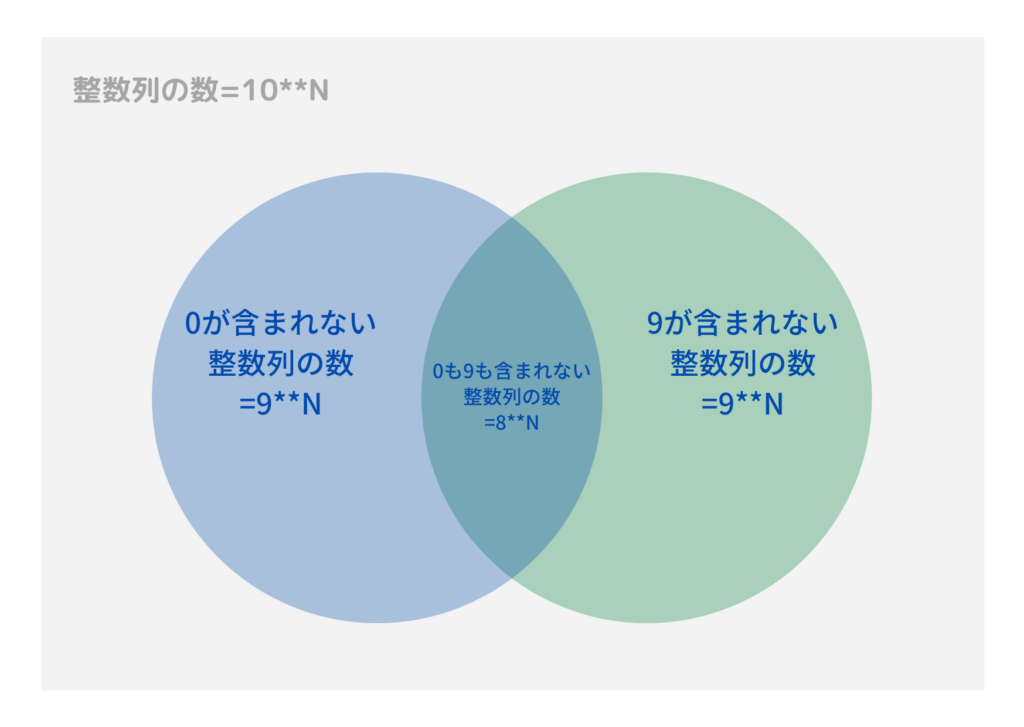
あとは最後にmodをとればOKでした。
# AtCoder Beginner Contest 178
# C - Ubiquity
N=int(input())
mod=10**9+7
print(((10**N)-(9**N)-(9**N)+(8**N))%mod)最近買った『プログラマの数学』にこの問題の類題が出ていて(第5章順列・組合わせ)読んでいたと思うので、これは解きたかったですねー!

プログラマの数学 第2版




コメント